Dalam matematika ada cara praktis dalam menentukan letak suatu benda yaitu dengan menggunakan koordinat kartesius. Bidang koordinat digunakan untuk menentukan letak titik. Pada bidang koordinat terdapat garis mendatar yang disebut sumbu X. Selain itu, juga terdapat garis tegak yang disebut sumbu Y. Setiap titik pada bidang koordinat dapat ditentukan letaknya berdasarkan jarak terhadap sumbu X dan sumbu Y.Perhatikan letak titik-titik pada bidang koordinat berikut.
Pada gambar bidang koordinat di atas, terdapat sumbu X dan sumbu Y. Sumbu X adalah garis mendatar yang dilengkapi dengan bilangan-bilangan bulat. Sumbu Y adalah garis tegak yang dilengkapi bilangan-bilangan bulat. Sumbu X dan sumbu Y digunakan untuk menentukan letak titik pada bidang koordinat. Bagaimana cara kita menentukan letak titik A?
Cara menentukan letak titik A adalah sebagai berikut.
Cara menentukan letak titik A adalah sebagai berikut.
- Perhatikan letak titik A.
- Tarik garis tegak melalui titik A dan memotong sumbu X pada bilangan -4. Bilangan -4 disebut absis.
- Tarik garis mendatar melalui titik A dan memotong sumbu Y pada bilangan 5. Bilangan 5 disebut ordinat.
- Koordinat titik A adalah pasangan bilangan (-4, 5) yang menyatakan letak titik A pada bidang koordinat.
Cara menentukan letak titik B :
- Perhatikan letak titik B.
- Tarik garis tegak melalui titik B dan memotong sumbu X pada bilangan -6. Bilangan -6 disebut absis.
- Tarik garis mendatar melalui titik B dan memotong sumbu Y pada bilangan -3. Bilangan -3 disebut ordinat.
- Koordinat titik B adalah pasangan bilangan (-6, -3) yang menyatakan letak titik B pada bidang koordinat.
Cara menentukan letak titik C:
- Perhatikan letak titik C.
- Tarik garis tegak melalui titik B dan memotong sumbu X pada bilangan 0. Bilangan 0 disebut absis.
- Titik C berada pada bilangan -2. Bilangan -2 disebut ordinat.
- Koordinat titik C adalah pasangan bilangan (0, -2) yang menyatakan letak titik C pada bidang koordinat.
Cara menentukan letak titik D :
- Perhatikan letak titik D.
- Tarik garis tegak melalui titik D dan memotong sumbu X pada bilangan 4. Bilangan 4 disebut absis.
- Tarik garis mendatar melalui titik D dan memotong sumbu Y pada bilangan 5. Bilangan 5 disebut ordinat.
- Koordinat titik D adalah pasangan bilangan (4, 5) yang menyatakan letak titik D pada bidang koordinat.
Cara menentukan letak titik E :
- Perhatikan letak titik E.
- Tarik E berada pada bilangan 6. Bilangan 6 disebut absis.
- Tarik garis mendatar melalui titik E dan memotong sumbu Y pada bilangan 0. Bilangan 0 disebut ordinat.
- Koordinat titik E adalah pasangan bilangan (6, 0) yang menyatakan letak titik E pada bidang koordinat.
Cara menentukan letak titik F :
- Perhatikan letak titik F.
- Tarik garis tegak melalui titik F dan memotong sumbu X pada bilangan 3. Bilangan 3 disebut absis.
- Tarik garis mendatar melalui titik F dan memotong sumbu Y pada bilangan -7. Bilangan -7 disebut ordinat.
- Koordinat titik F adalah pasangan bilangan (3, -7) yang menyatakan letak titik F pada bidang koordinat.
Untuk menggambar bangun datar juga dapat menggunakan bidang koordinat. Cara menggambar bangun datar pada bidang koordinat tidak jauh berbeda dengan menentukan letak titik pada bidang koordinat. Hanya saja jika ingin membuat bangun datar maka ada langkah lanjutannya, yaitu seteah menentukan titik-titik tersebut kemudian titik-titik dihubungkan antara titik satu dengan titik lainnya dengan menggunakan garis sehingga membentuk bidang datar yang dikehendaki.
Contoh Soal :
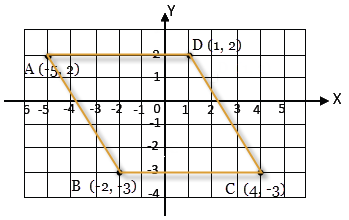
Diketahui koordinat titik-titik berikut. A (-5, 2), B (-2, -3), C (4, -3), dan D (1, 2). Tentukan letak titik A, B, C, dan D pada bidang koordinat berikut.Kemudian, hubungkan titik A dan B, B dan C, C dan D, serta A dan D. Bangun apakah ABCD?Berdasarkan gambar di atas kita juga dapat menentukan koordinat bangun datar yang lainnya, misalnya :
| No. | Nama Bangun | Koordinat Titik Sudut |
| 1. | Persegi Panjang | E (-5, 2), F (-5, -3), G ( 2, -3), dan H (2, 2) |
| 2. | Persegi | I (-3, 2), J (-3, -2), K (1, -2), dan L (1, 2) |
| 3. | Segitiga Samakaki | M (-3, 2), N (-5, -4), dan O (-1, -4) |
| 4. | Trapesium | P (-5, 2), Q (-5, -3), R (5, -3), dan S (1, 2) |
| 5. | Layang-layang | T (5, 0), U (-3, -2), V (5, 0), dan W (-3, 2) |